SelectionSort

算法思路及原理

首先在所有未排序的元素中找出最小值，放到首位，然后在剩余未排序的元素中找到最小值，放到第二位置，以次类推

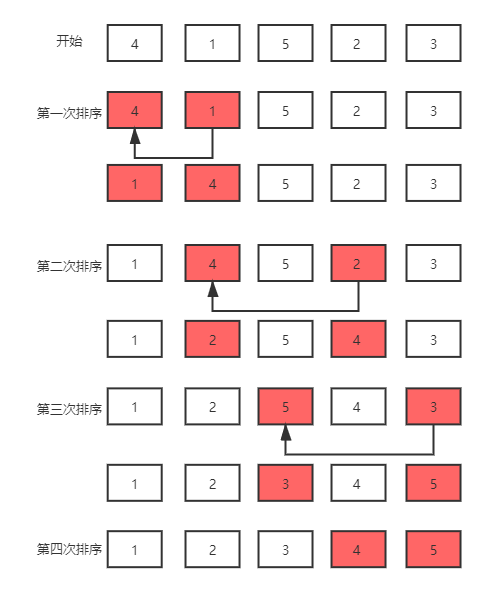
算法分析

时间复杂度

选择排序的外层为 n-1 次，比较操作为 n(n-1)/2 次。时间复杂度为O(n^2），比较次数与关键字的初始状态无关，总的比较次数N=(n-1）+(n-2）+…+1=n*(n-1）/2。交换次数O(n），最好情况是，已经有序，交换0次；最坏情况交换n-1次，逆序交换n/2次。交换次数比冒泡排序少多了，由于交换所需CPU时间比比较所需的CPU时间多，n值较小时，选择排序比冒泡排序快。

空间复杂度

不需要额外的空间，O(1)。

稳定性

选择排序是给每个位置选择当前元素最小的，比如给第一个位置选择最小的，在剩余元素里面给第二个元素选择第二小的，依次类推，直到第n-1个元素，第n个元素不用选择了，因为只剩下它一个最大的元素了。那么，在一趟选择，如果一个元素比当前元素小，而该小的元素又出现在一个和当前元素相等的元素后面，那么交换后稳定性就被破坏了。举个例子，序列5 8 5 2 9，我们知道第一遍选择第1个元素5会和2交换，那么原序列中两个5的相对前后顺序就被破坏了，所以选择排序是一个不稳定的排序算法。

实现代码

/*
* 选择排序
* */
public class SelectionSort {
    public static void main(String[] args) {
        int[] arr = {2, 4, 6, 1, 5, 3, 7};
        sort(arr);
    }

    static void sort(int[] arr) {
        for (int i = 0; i < arr.length - 1; i++) {
            int minPos = i;
            for (int j = i+1; j < arr.length; j++) {
                minPos = arr[j] < arr[minPos] ? j : minPos;
            }
            swap(arr, i, minPos);
        }
    }

    static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;

    }
}

算法优化

在每次循环时，选择最大和最小值同时进行排序，最小值放首位，最大值放末尾。但是当首位等于最大值和末尾等于最小值时要特殊考虑。

public class SelectionSort2 {
    public static void main(String[] args) {
        int[] arr = {2, 4, 6, 1, 5, 3, 7};
        sort(arr);
    }

    static void sort(int[] arr) {
        for (int i = 0; i < arr.length-1; i++) {
            int minPos = i;
            int maxPos = arr.length-i-1;

            for (int j = i; j < arr.length-i; j++) {
                if (arr[j] < arr[minPos]) minPos = j;
                if (arr[j] > arr[maxPos]) maxPos = j;
            }

            if (i == maxPos && arr.length-i-1 != minPos) {
                swap(arr, arr.length - i - 1, maxPos);
                swap(arr, i, minPos);
            } else if (i != maxPos && arr.length-i-1 == minPos) {
                swap(arr, i, minPos);
                swap(arr, arr.length - i - 1, maxPos);
            } else if (i == maxPos && arr.length-i-1 == minPos) {
                swap(arr, maxPos, minPos);
            } else {
                swap(arr, i, minPos);
                swap(arr, arr.length - i - 1, maxPos);
            }
        }
    }
    static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}