InsertionSort

算法思路及原理

插入排序是指在待排序的元素中，假设前面n-1(其中n>=2)个数已经是排好顺序的，现将第n个数插到前面已经排好的序列中，然后找到合适自己的位置，使得插入第n个数的这个序列也是排好顺序的。按照此法对所有元素进行插入，直到整个序列排为有序的过程。

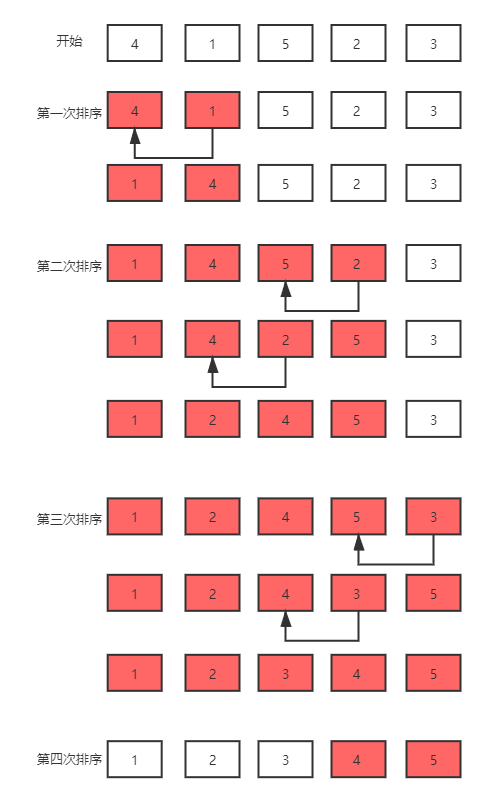
算法分析

时间复杂度

当元素初始状态为正序时，只需要当前元素与前一元素作比较就可以结束排序，一共需要比较n-1次，O(n);
当元素初始状态为逆序时，需要比较并交换每一次的相邻元素，O(n^2);
故平均时间复杂度为o(n^2)。

空间复杂度

不需要额外空间，O(1)。

稳定性

插入排序就是把后一个元素往前调。比较是相邻的两个元素比较，交换也发生在这两个元素之间。所以，如果两个元素相等，是不会再交换的；如果两个相等的元素没有相邻，那么即使通过前面的两两交换把两个相邻起来，这时候也不会交换，所以相同元素的前后顺序并没有改变，所以插入排序是一种稳定排序算法。

适用性

样本小且基本有序的时候效率很高

实现代码

public class InsertionSort {
    public static void main(String[] args) {
        int[] arr = {3, 5, 4, 6, 8, 7, 2, 1};
        sort(arr);
    }

    static void sort(int[] arr) {
        for (int i = 1; i < arr.length; i++) {
            for (int j = i; j > 0; j--) {
                if (arr[j] < arr[j-1]) {
                    swap(arr, j, j-1);
                }
            }
        }
    }

    static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

算法优化

不使用swap方法，设置一个temp变量来存储需要排序的元素，如果temp比前一个元素小，就直接arr[j] = arr[j-1]，依次向前比较，直到temp比前一个元素大，就让对应位置的值为temp。

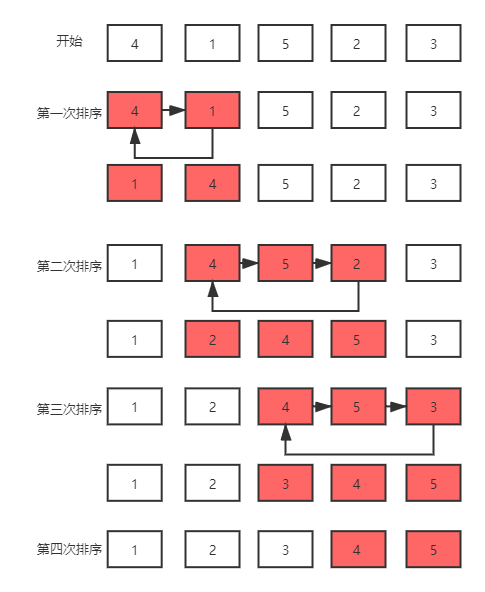
public class InsertionSort2 {
    public static void main(String[] args) {
        int[] arr = {3, 5, 4, 6, 8, 7, 2, 1};
        sort(arr);
    }

    static void sort(int[] arr) {
        for (int i = 1; i < arr.length; i++) {
            int temp = arr[i];
            int s = i;
            for (int j = i; j > 0; j--) {
                if (temp < arr[j-1]) {
                    arr[j] = arr[j-1];
                    s = j-1;
                }
            }
            arr[s] = temp;
        }
    }