剑指Offer
Kang Lv3
 2021-04-14 19:55:54      11.5k 字  54 分钟  

数组

  • 数组的查找问题先试试二分查找和双指针

剑指 Offer 03. 数组中重复的数字

HashSet/哈希表

算法流程
  1. 初始化：新建一个 HashSet ，哈希表只能存储不重复的数据；
  2. 遍历数组，如果该数字不存在哈希表中，则添加到哈希表中；如果已经被添加到哈希表中了，说明改数字为重复数字，就返回改数字；
  3. 返回值：最后必须加一个 return 语句，不然报错。
复杂度分析
  • 时间复杂度O(N):遍历数组的耗费 O(N) ，查找和添加元素为 O(N) ；
  • 空间复杂度O(N): HashSet 耗费 O(N) 的空间
代码
1
2
3
4
5
6
7
8
9
10
class Solution {
    public int findRepeatNumber(int[] nums) {
        Set<Integer> hs = new HashSet<>();
        for (int num : nums) {
            if (hs.contains(num)) return num;
            hs.add(num);
        }
        return -1;
    }
}

剑指 Offer 04. 二维数组中的查找

线性查找

算法流程

二维数组中的查找

  1. 空值处理：当 matrix 为空或 matrix 长度为0时，直接返回 false 即可。
  2. 对于右上角元素而言，如果它大于 target，则查找位置向左移一列，如果它小于target，则查找位置向下移一行。
复杂度分析
  • 时间复杂度O(m+n):最多移动m+n次(m行n列时)；
  • 空间复杂度O(1):只需要 i 和 j 两个指针的空间。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public boolean findNumberIn2DArray(int[][] matrix, int target) {
        if (matrix == null || matrix.length == 0) return false;
        int i = 0;
        int j = matrix[0].length - 1;
        while (i<=matrix.length-1 && j>=0) {
            if (matrix[i][j] == target) return true;
            if (matrix[i][j] > target) j--;
            else i++;
        }
        return false;
    }
}

剑指 Offer 05. 替换空格

使用现有方法

算法流程
  1. 直接使用 String 的 replace 方法
代码
1
2
3
4
5
class Solution {
    public String replaceSpace(String s) {
        return s.replace(" ", "%20");
    }
}

StringBuilder

算法流程
  1. 初始化：java中的字符串是不可变的，不能直接修改。我们使用 StringBuilder 来操作，StringBuffer 耗费时间长一点；
  2. 遍历字符串：遍历整个字符串，如果遇到空格，向 StringBuffer 中 append %20 ；否则，就 append 这个字符；
  3. 返回值：将 StringBuilder 转换为 String 并return。
复杂度分析
  • 时间复杂度O(N):需要遍历整个字符串 O(N) ，append 时间复杂度为 O(1) ；
  • 空间复杂度O(N):最少需要N个空间(没有空格)，最多需要3N个空间(全都是空格)。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public String replaceSpace(String s) {
        StringBuilder sb = new StringBuilder();
        for (char c : s.toCharArray()) {
            if (c == ' ') sb.append("%20");
            else sb.append(c);
        }
        return sb.toString();
    }
}

class Solution {
    public String replaceSpace(String s) {
        StringBuilder sb = new StringBuilder();
        for (int i=0; i<s.length(); i++) {
            if (s.charAt(i) == ' ') sb.append("%20");
            else sb.append(s.charAt(i));
        }
        return sb.toString();
    }
}

数组

算法流程
  1. 初始化：创建一个3倍长的数组，这样可以保证存放替换后的所有字符
  2. 遍历字符串:
    1. 如果字符为空格，则令array[size++]=’%’,array[size++]=’2’,array[size++]=’0’
    2. 否则，就令array[size++]=字符
  3. 截取数组中0-size长度为返回的数组
复杂度
  • 时间复杂度：O(n)。需要遍历整个字符串一遍
  • 空间复杂度：O(n)。需要额外字符串长度+空格数*2的额外空间
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public String replaceSpace(String s) {
        int length = s.length();
        char[] array = new char[length*3];
        int size = 0;
        for (int i = 0; i < length; i++) {
            char c = s.charAt(i);
            if (c == ' ') {
                array[size++] = '%';
                array[size++] = '2';
                array[size++] = '0';
            } else {
                array[size++] = c;
            }
        }
        String newStr = new String(array, 0, size);
        return newStr;
    }
}

剑指 Offer 11. 旋转数组的最小数字

二分查找

算法流程
  1. 初始化：设置一个初始左右边界，left=0，right=nums.length-1
  2. 循环二分：当left<right时，并求得mid=left+(right-left)/2
    1. 若nums[mid]<nums[right]时，right=mid；
    2. 若nums[mid]>nums[right]时，left=mid+1；
    3. 当相等时，right -= 1；
  3. return nums[left]
复杂度
  • 时间复杂度：O(logn)。
  • 空间复杂度：O(1)
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int minArray(int[] numbers) {
        int left = 0;
        int right = numbers.length-1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (numbers[mid] < numbers[right]) right = mid;
            else if (numbers[mid] > numbers[right]) left = mid + 1;
            else right -= 1;
        }
        return numbers[left];
    }
}

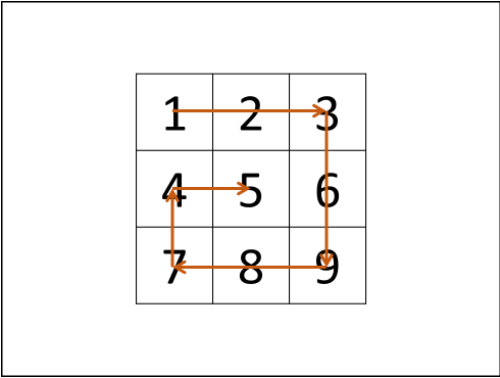
剑指 Offer 29. 顺时针打印矩阵

分层

算法流程
  1. 空值处理：当 matrix 为空或 matrix 长度为0时，直接返回空列表[ ]即可。
  2. 初始化：矩阵左、右、上、下四个边界 left, right, top, bottom，用于打印的结果列表 result。
  3. 循环打印：“从左向右、从上向下、从右向左、从下向上” 四个方向循环，每个方向打印中做以下三件事；
    • 根据边界打印，即将元素按顺序添加至列表 result 尾部；
    • 边界向内收缩1（代表已被打印）；
    • 判断是否打印完毕（边界是否相遇），若打印完毕则跳出。
  4. 返回值：返回 result 即可。

顺时针打印矩阵

复杂度分析
  • 时间复杂度O(MN)：需要遍历每一个元素O(m*n)(m行n列)；
  • 空间复杂度O(1)：不需要额外的空间。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public int[] spiralOrder(int[][] matrix) {
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) return new int[0];

        int left = 0, right = matrix[0].length -1, top = 0, bottom = matrix.length - 1;
        int[] result = new int[(right+1)*(bottom+1)];
        int x = 0;
        while (true) {
            for (int i=left; i<=right; i++) result[x++] = matrix[top][i];
            if (++top > bottom) break;
            for (int i=top; i<=bottom; i++) result[x++] = matrix[i][right];
            if (left > --right) break;
            for (int i=right; i>=left; i--) result[x++] = matrix[bottom][i];
            if (top > --bottom) break;
            for (int i=bottom; i>=top; i--) result[x++] = matrix[i][left];
            if (++left > right) break;
        }
        return result;
    }
}

剑指 Offer 42. 连续子数组的最大和

动态规划

算法流程
  1. 初始化
  2. 遍历数组：
    1. 如果前几个数的和pre 加 当前数x 与 当前数x 进行比较时，选择较大的那个值，即 max(pre+x, x)；
    2. 当前最大数组的和maxvalue 与 刚得到的数组的和pre 进行比较时，选择较大的那个值，即 max(maxvalue, pre)。
  3. return maxvalue;
复杂度
  • 时间复杂度：O(n)。遍历整个数组
  • 空间复杂度：O(1)。
代码
1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public int maxSubArray(int[] nums) {
        int pre = 0;
        int maxValue = nums[0];
        for (int num : nums) {
            pre = Math.max(pre+num, num);
            maxValue = Math.max(pre, maxValue);
        }
        return maxValue;
    }
}

分治

还没看

剑指 Offer 47. 礼物的最大价值

动态规划(二维数组)

算法流程
  1. 循环遍历整个二维数组，m=grid.length，n=grid[0].length
    1. 当 i==0 && j==0 时，grid[i][j] = grid[0][0];
    2. 当只有 i==0 时，只有左侧有格子，grid[i][j] += grid[i][j-1];
    3. 当只有 j==0 时，只有上侧有格子，grid[i][j] += grid[i-1][j];
    4. 当 i!=0 && j!=0 时，选择左侧和上侧格子中较大的值，grid[i][j] += max(grid[i][j-1], grid[i-1][j]);
  2. 返回最右下角位置的值，return grid[m-1][n-1]
复杂度
  • 时间复杂度：O(MN)。M,N为数组的行和列，需要遍历整个数组
  • 空间复杂度：O(1)。直接修改原来的数组的值
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int maxValue(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        for (int i=0; i<m; i++) {
            for (int j=0; j<n; j++) {
                if (i == 0 && j == 0) grid[i][j] = grid[0][0];
                else if (i == 0) grid[i][j] += grid[i][j-1];
                else if (j == 0) grid[i][j] += grid[i-1][j];
                else grid[i][j] += Math.max(grid[i-1][j], grid[i][j-1]);
            }
        }
        return grid[m-1][n-1];
    }
}

剑指 Offer 50. 第一个只出现一次的字符

哈希表

算法流程
  1. 初始化：创建一个空的哈希表，存储出现的字符和对应出现的次数；
  2. 遍历：遍历整个字符串，把每个字符存放到哈希表中；
  3. 按照字符串的顺序，查找出现次数为1的字符；
  4. 返回值：如果传入字符串为空，则返回 ' ' 。
复杂度分析
  • 时间复杂度O(N)：需要遍历整个字符串；
  • 空间复杂度O(1)：额外创建一个哈希表，因为传入的字符只有小写字母，所以所需空间最大为26。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public char firstUniqChar(String s) {
        Map<Character, Integer> hsm = new HashMap<>();
        for (char str : s.toCharArray()) {
            hsm.put(str, hsm.getOrDefault(str, 0) + 1);
        }

        for (char str : s.toCharArray()) {
            if (hsm.get(str) == 1) return str;
        }
        return ' ';
    }
}
优化

将 Map<Character, Integer> 改为 Map<Character, Boolean>
若哈希表hsm中不包含键(key) c ：则向 hsm 中添加键值对 (c, True) ，代表字符 c 的数量为1；
若哈希表hsm中已经包含键(key) c ：则修改键 c 的键值对为 (c, False) ，代表字符 c 的数量>1。

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public char firstUniqChar(String s) {
        HashMap<Character, Boolean> hsm = new HashMap<>();
        char[] ch = s.toCharArray();
        for(char c : ch)
            hsm.put(c, !hsm.containsKey(c));
        for(char c : ch)
            if(hsm.get(c)) return c;
        return ' ';
    }
}

剑指 Offer 53 - I. 在排序数组中查找数字 I

数组遍历

算法流程
  1. 初始化：设置一个记录target出现次数的计数变量count
  2. 遍历数组一遍，遇到与target相同的数字，count++
  3. return count
复杂度
  • 时间复杂度：O(n)。需要遍历一遍数组
  • 空间复杂度：O(1)。不需要额外的空间
代码
1
2
3
4
5
6
7
8
9
class Solution {
    public int search(int[] nums, int target) {
        int count = 0;
        for (int i=0; i<nums.length; i++) {
            if (nums[i] == target) count++;
        }
        return count;
    }
}

剑指 Offer 53 - II. 0～n-1中缺失的数字

二分查找

算法流程
  1. 初始化：设置两个边界值，left=0，right=nums.length-1
  2. 循环二分：当left>right时结束
    1. m=(left+right)/2
    2. 若nums(m)=m,则左半部分不缺少数值，令left=m+1
    3. 否则，则右半部分不缺少数值，令right=m
  3. return left
复杂度
  • 时间复杂度：O(logn)。
  • 空间复杂度：O(1)。
代码
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int missingNumber(int[] nums) {
        int left = 0;
        int right = nums.length;
        while (left < right) {
            int m = (left + right)/2;
            if (nums[m] == m) left = m + 1;
            else right = m;
        }
        return left;
    }
}

栈队列堆

剑指 Offer 06. 从头到尾打印链表

栈和指针

算法流程
  1. 初始化：stack栈用来存放链表的节点，temp指向链表的头结点；
  2. 当temp指向的元素非空时，将指针指向的节点压入栈中，将指针指向下一个节点。
  3. size = stack.size()，获得栈的大小，创建一个数组arr，大小为size；
  4. 将其逐个出栈存入到arr中，arr[index] = stack.pop().val。
复杂度分析
  • 时间复杂度：O(n)。正向遍历一遍链表，然后弹出全部节点，等于反向遍历一遍。
  • 空间复杂度：O(n)。需要占用额外等同于链表的栈空间。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public int[] reversePrint(ListNode head) {
        Stack<ListNode> stack = new Stack<>();
        ListNode temp = head;
        while (temp != null) {
            stack.push(temp);
            temp = temp.next;
        }

        int size = stack.size();
        int[] arr = new int[size];
        for (int i=0; i<size; i++) {
            arr[i] = stack.pop().val;
        }
        return arr;
    }
}

剑指 Offer 09. 用两个栈实现队列

双栈

算法流程
  1. 初始化：stackIn 栈用来处理入栈（push）操作，stackOut 栈用来处理出栈（pop）操作。
  2. 一个元素进入 stackIn 栈之后，出栈的顺序需要被反转。当元素要出栈时，需要先进入 stackOut 栈，此时元素出栈顺序再一次被反转，因此出栈顺序就和最开始入栈顺序是相同的，先进入的元素先退出，这正是队列的顺序。
复杂度分析
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class CQueue {
    private Stack<Integer> stackIn;
    private Stack<Integer> stackOut;

    public CQueue() {
        stackIn = new Stack<>();
        stackOut = new Stack<>();
    }
    
    public void appendTail(int value) {
        stackIn.push(value);
    }
    
    public int deleteHead() {
        // 如果stackOut不为空
        if(!stackOut.isEmpty()){
            return stackOut.pop();
        }else{
            while(!stackIn.isEmpty()){
                stackOut.push(stackIn.pop());
            }
        return stackOut.isEmpty() ? -1 : stackOut.pop();
        }
    }
}

剑指 Offer 30. 包含min函数的栈

双栈

算法流程
  1. 初始化：设计两个栈，一个存放数据dataStack，一个作为辅助栈存放最小值minStack；
  2. push：当minSatck为空或栈顶的元素比push的数据x大时，就将x放入minStack中；
  3. pop：取出dataStack的栈顶元素，如果该元素等于minStack栈顶元素，就也取出minStack的栈顶元素，使辅助栈minStack的栈顶保持为已有元素的最小值；
  4. min和top：使用peek获得minStack和dataStack的栈顶即可。
复杂度分析
  • 复杂度：几个方法的复杂度都为O(1)。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class MinStack {
    private Stack<Integer> dataStack;
    private Stack<Integer> minStack;
    /** initialize your data structure here. */
    public MinStack() {
        dataStack = new Stack<Integer>();
        minStack = new Stack<>();
    }
    
    public void push(int x) {
        dataStack.push(x);
        if (minStack.empty() || minStack.peek()>=x) {
            minStack.push(x);
        }
    }
    
    public void pop() {
        if (dataStack.pop().equals(minStack.peek())) {
            minStack.pop();
        }
    }
    
    public int top() {
        return dataStack.peek();
    }
    
    public int min() {
        return minStack.peek();
    }
}

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack obj = new MinStack();
 * obj.push(x);
 * obj.pop();
 * int param_3 = obj.top();
 * int param_4 = obj.min();
 */

剑指 Offer 31. 栈的压入、弹出序列

栈

算法流程
  1. 初始化：创建一个辅助栈，用于模拟出入栈过程，创建一个 i=0，用于计数
  2. 遍历：遍历整个压栈过程，每次入栈一个元素，判断栈顶元素是否等于出站序列 popped[i] ，如果是的话，则执行出栈操作并将 i++ ；
  3. 返回值：判断stack是否为空，若为空，表示是对应压入序列的弹出序列
复杂度分析
  • 时间复杂度O(N)：每个元素最多入栈一次，出栈一次。
  • 空间复杂度O(N)：使用了额外的一个最大为N的辅助栈。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public boolean validateStackSequences(int[] pushed, int[] popped) {
        Stack<Integer> stack = new Stack<>();
        int i = 0;
        for (int num : pushed) {
            stack.push(num);
            while (!stack.empty() && stack.peek()==popped[i]) {
                stack.pop();
                i++;
            }
        }
        return stack.empty();
    }
}

剑指 Offer 40. 最小的k个数

排序

算法流程
  1. 初始化：创建一个保存前k个数的数组res；
  2. 对arr数组进行排序 Arrays.sort(arr) ;
  3. 取出前k个数放入res中，并返回res。
复杂度分析
  • 时间复杂度O(NlogN)：算法的复杂度即排序的复杂度，O(NlogN)；
  • 空间复杂度O(logN)：排序所需的额外空间复杂度为 O(logN)。
代码
1
2
3
4
5
6
7
8
9
10
class Solution {
    public int[] getLeastNumbers(int[] arr, int k) {
        Arrays.sort(arr);
        int[] res = new int[k];
        for (int i=0; i<k; i++) {
            res[i] = arr[i];
        }
        return res;
    }
}

链表

剑指 Offer 22. 链表中倒数第k个节点

stack

算法流程
  1. 初始化：创建一个stack
  2. 将ListNode逐个压入栈中，栈中的顺序就是ListNode的逆序
  3. 逐个弹出ListNode，第k个弹出的就是倒数第k个节点
复杂度
  • 时间复杂度：O(n)。需要遍历链表一遍，弹出时遍历前K个
  • 空间复杂度：O(n)。需要链表长度的栈的额外空间
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode getKthFromEnd(ListNode head, int k) {
        Stack<ListNode> stack = new Stack<>();
        ListNode curr = head;
        while (curr != null) {
            stack.push(curr);
            curr = curr.next;
        }
        for (int i=0; i<k-1; i++) {
            stack.pop();
        }
        return stack.pop();
    }
}

顺序查找

算法流程
  1. 初始化：新建size，用来存储链表的长度
  2. 循环整个链表，获得链表的长度
  3. for循环从head一直到size-k的位置，并返回
复杂度
  • 时间复杂度：O(n)。求链表长度是遍历一遍，获取倒数第k个节点时，遍历n-k个节点
  • 空间复杂度：O(1)。不需要额外的空间
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode getKthFromEnd(ListNode head, int k) {
        int size = 0;
        ListNode curr = head;
        while (curr != null) {
            curr = curr.next;
            size++;
        }
        for (int i = 0; i < size-k; i++) {
            head = head.next;
        }
        return head;
    }
}

双指针

算法流程
  1. 初始化：新建两个指针，fast和slow
  2. 让fast指针指向第k个节点，slow指针指向第0个节点。当fast指针指向最后节点时，slow节点就会指向第n-k个节点
复杂度
  • 时间复杂度：O(n)。只需对链表遍历一遍
  • 空间复杂度：O(n)。不需要额外空间
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode getKthFromEnd(ListNode head, int k) {
        ListNode fast = head;
        ListNode slow = head;
        for (int i = 0; i < k; i++) {
            fast = fast.next;
        }
        while (fast!=null) {
            fast = fast.next;
            slow = slow.next;
        }
        return slow;
    }
}

剑指 Offer 24. 反转链表

迭代

算法流程
  1. 初始化：设置两个节点，一个为当前节点cur，一个为前一节点pre；
  2. 反转链表时，当前节点cur的next指向pre，并将pre指向下一节点，cur指向下一节点。
算法复杂度
  • 时间复杂度：O(n)，只需遍历链表一遍
  • 空间复杂度：O(1)
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode pre = null;
        ListNode cur = head;
        while (cur != null) {
            ListNode next = cur.next;
            cur.next = pre;
            pre = cur;
            cur = next;
        }
        return pre;
    }
}

剑指 Offer 25. 合并两个排序的链表

双指针

算法流程
  1. 初始化：设置一个新的ListNode头结点start和cur。
  2. 循环合并：当l1或L2为空时跳出；
    1. 当l1.val<l2.val时：cur的next节点为l1，并l1指向自身下一节点
    2. 当l1.val>=l2.val时：cur的next节点为l2，并l2指向自身下一节点
    3. cur指向下一节点
  3. 合并剩余尾部：跳出时有两种情况，即l1为空或l2为空
    1. 若l1！=null，将l1添加到cur.next
    2. 否则，将l2添加到cur.next
  4. return start节点的next
复杂度
  • 时间复杂度：O(n)。将两个链表遍历一遍
  • 空间复杂度：O(n)。需要额外两个链表长度之和的空间
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        ListNode cur = new ListNode(0);
        ListNode start = cur;
        while (l1!=null && l2!=null) {
            if (l1.val < l2.val) {
                cur.next = l1;
                l1 = l1.next;
                cur = cur.next;
            } else {
                cur.next = l2;
                l2 = l2.next;
                cur = cur.next;
            }
        } 
        cur.next = l1!=null ?l1:l2;
        return start.next;
    }
}

剑指 Offer 35. 复杂链表的复制

回溯 + 哈希表

算法流程
  1. 不大会
复杂度
  • 时间复杂度：O(n)。对于每个节点，我们至多访问其next节点和random节点各一次，平均每个节点被访问2次
  • 空间复杂度：O(n)。额外存储一个哈希表，大小为n
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/*
// Definition for a Node.
class Node {
    int val;
    Node next;
    Node random;

    public Node(int val) {
        this.val = val;
        this.next = null;
        this.random = null;
    }
}
*/
class Solution {
    Map<Node, Node> cachedNode = new HashMap<>();
    public Node copyRandomList(Node head) {
        if (head == null) {
            return null;
        }
        if (!cachedNode.containsKey(head)) {
            Node headNew = new Node(head.val);
            cachedNode.put(head, headNew);
            headNew.next = copyRandomList(head.next);
            headNew.random = copyRandomList(head.random);
        }
        return cachedNode.get(head);
    }
}

迭代 + 节点拆分

算法流程
复杂度
  • 时间复杂度：O(n)。需要遍历链表三遍
  • 空间复杂度：O(1)。？？？
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/*
// Definition for a Node.
class Node {
    int val;
    Node next;
    Node random;

    public Node(int val) {
        this.val = val;
        this.next = null;
        this.random = null;
    }
}
*/
class Solution {
    public Node copyRandomList(Node head) {
        if (head == null) {
            return null;
        }

        for (Node node=head; node!=null; node=node.next.next) {
            Node nodeNew = new Node(node.val);
            nodeNew.next = node.next;
            node.next = nodeNew;
        }
        for (Node node=head; node!=null; node=node.next.next) {
            Node nodeNew = node.next;
            nodeNew.random = (node.random!=null) ? node.random.next:null;
        }

        Node headNew = head.next;
        for (Node node=head; node!=null; node=node.next) {
            Node nodeNew = node.next;
            node.next = node.next.next;
            nodeNew.next = (nodeNew.next != null) ? nodeNew.next.next : null;
        }
        return headNew;
    }
}

字符串

剑指 Offer 58 - II. 左旋转字符串

使用现有方法

算法流程
  1. 使用substring()方法进行获取部分字符串，然后使用+进行拼接
复杂度
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)。两个字符串的总长度为N。
代码
1
2
3
4
5
class Solution {
    public String reverseLeftWords(String s, int n) {
        return s.substring(n, s.length()) + s.substring(0, n);
    }
}

StringBuilder

算法流程
  1. 初始化：new一个新的StringBuilder存放字符串s中的字符
  2. 将n到末尾的字符先append到StringBuilder中
  3. 再将0到n的字符append到StringBuilder中
复杂度
  • 时间复杂度：O(n)。遍历一遍整个字符串
  • 空间复杂度：O(n)。StringBuilder所占用大小为字符串长度
代码
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public String reverseLeftWords(String s, int n) {
        StringBuilder sb = new StringBuilder();
        for (int i = n; i < s.length(); i++) {
            sb.append(s.charAt(i));
        }
        for (int i = 0; i < n; i++) {
            sb.append(s.charAt(i));
        }
        return sb.toString();
    }
}

树

剑指 Offer 26. 树的子结构

递归

算法流程

不大会

复杂度
  • 时间复杂度：O(mn)。
  • 空间复杂度：O(n)
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public boolean isSubStructure(TreeNode A, TreeNode B) {
        return (A != null && B != null) && (recru(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B));
    }
    boolean recru(TreeNode L, TreeNode R) {
        if (R == null) return true;
        if (L == null || L.val != R.val) return false;
        return recru(L.left, R.left) && recru(L.right, R.right);
    }
}

剑指 Offer 27. 二叉树的镜像

递归

算法流程
  1. 从根节点开始，递归地对树进行遍历，并从叶节点先开始翻转得到镜像
  2. 如果当前遍历到的节点root的左右两棵树都已经翻转得到镜像，那么我们只需要交换两颗子树的位置，即可得到以root为根节点的整棵子树的镜像
复杂度
  • 时间复杂度：O(n)。会遍历每一个节点，并交换每一个节点的两棵子树。
  • 空间复杂度：O(n)。平衡二叉树为O(logn)，最坏情况下（链状），复杂度为O(n).
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode mirrorTree(TreeNode root) {
        if (root == null) return root;
        TreeNode left = mirrorTree(root.left);
        TreeNode right = mirrorTree(root.right);
        root.left = right;
        root.right = left;
        return root;
    }
}

剑指 Offer 28. 对称的二叉树

算法流程

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public boolean isSymmetric(TreeNode root) {
        return root == null ? true : recur(root.left, root.right);
    }

    boolean recur(TreeNode L, TreeNode R) {
        if (L == null && R == null) return true;
        if (L == null || R == null || L.val != R.val) return false;
        return recur(L.left, R.right) && recur(L.right, R.left);
    }
}

剑指 Offer 32 - I. 从上到下打印二叉树

层序遍历 BFS

算法流程
  1. 初始化：打印结果为arr = []，包含根节点的队列queue = [root];
  2. BFS循环：当队列queue为空时跳出
    1. 队首元素出队，记为node
    2. 将node.val添加到链表al的尾部
    3. 将node的左右子树加入队列queue
  3. 将链表al转换为数组并返回
复杂度
  • 时间复杂度：O(n)。
  • 空间复杂度：O(n)
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int[] levelOrder(TreeNode root) {
        if (root == null) return new int[0];
        Queue<TreeNode> queue = new LinkedList<>() {{add(root);}};
        ArrayList<Integer> al = new ArrayList<>();
        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();
            al.add(node.val);
            if (node.left != null) queue.add(node.left);
            if (node.right != null) queue.add(node.right);
        }

        int[] arr = new int[al.size()];
        for (int i=0; i<al.size(); i++) {
            arr[i] = al.get(i);
        }
        return arr;
    }
}

剑指 Offer 32 - II. 从上到下打印二叉树 II

BFS(广度优先搜索)

算法流程
  1. 初始化：打印结果为res=[]，包含根节点的队列queue=[root]
  2. BFS循环：当queue为空时跳出
    1. 建一个临时ArrayList tmp
    2. for (int i=queue.size(); i>0; i–)
      1. 队首元素出队，记为node
      2. 将node.val加入tmp中
      3. 若存在左右子树，加入队列queue
    3. res.add(tmp)
  3. return res
复杂度
  • 时间复杂度：O(n)。将每一个节点都会被进入队列一次
  • 空间复杂度：O(n)。平衡二叉树时，最多有N/2个节点进去队列
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        // if (root == null) return new ArrayList<List<Integer>>();
        Queue<TreeNode> queue = new LinkedList<>() {{ if (root!=null) add(root); }};
        List<List<Integer>> res = new ArrayList<>();
        while (!queue.isEmpty()) {
            List<Integer> tmp = new ArrayList<>();
            for (int i=queue.size(); i>0; i--) {
                TreeNode node = queue.poll();
                tmp.add(node.val);
                if (node.left != null) queue.add(node.left);
                if (node.right != null) queue.add(node.right);
            }
            res.add(tmp);
        }
        return res;
    }
}

剑指 Offer 32 - III. 从上到下打印二叉树 III

BFS

流程算法
复杂度
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>() {{if(root!=null) add(root);}};
        List<List<Integer>> res = new ArrayList<>();
        boolean flag = false;
        while (!queue.isEmpty()) {
            LinkedList<Integer> tmp = new LinkedList<>();
            for (int i=queue.size(); i>0; i--) {
                TreeNode node = queue.poll();
                if (res.size()%2 == 0) tmp.addLast(node.val);
                else tmp.addFirst(node.val);
                if (node.left != null) queue.add(node.left);
                if (node.right != null) queue.add(node.right);
            }
            res.add(tmp);
        }
        return res;
    }
}

动态规划

剑指 Offer 10- I. 斐波那契数列

递归

算法流程
  1. 写出跳出条件：
    1. if(n==0) return 0;
    2. if(n==1) return 1;
  2. return fib(n-1) + fib(n-2);
复杂度
  • 时间复杂度：O(2^n)。第一想到的就是使用递归，但是递归的复杂度是指数级
  • 空间复杂度：O(1)。
代码
1
2
3
4
5
6
7
class Solution {
    public int fib(int n) {
        if (n == 0) return 0;
        if (n == 1) return 1;
        return fib(n-1) + fib(n-2);
    }
}

动态规划

算法流程
  1. 设置跳出条件：if(n<2) return n;
  2. 初始化：p=0,q=0,r=1
  3. 循环，直到n
    1. p=q;
    2. q=r
    3. r=p+q
  4. return r
复杂度
  • 时间复杂度：O(n)。
  • 空间复杂度：O(1)。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int fib(int n) {
        int MOD = 1000000007;
        if (n < 2) return n;

        int p = 0;
        int q = 0;
        int r = 1;
        for (int i=2; i<=n; i++) {
            p = q;
            q = r;
            r = (p + q) % MOD;
        }
        return r;
    }
}

通项公式

算法流程

找出斐波那契数列的通项公式

复杂度
  • 时间复杂度：O(1)。
  • 空间复杂度：O(1)。
代码
1
2
3
4
5
6
7
8
9
10
class Solution {
    double fac1 = 1 / Math.sqrt(5);
    double fac2 = 0.5 + Math.sqrt(5) / 2;
    double fac3 = 0.5 - Math.sqrt(5) / 2;
    
    public int fib(int n) {
        if (n < 2) return n;
        return (int) (fac1 * (Math.pow(fac2, n) - Math.pow(fac3, n)));
    }
}

剑指 Offer 10- II. 青蛙跳台阶问题

动态规划

算法流程
  1. 设跳上n级台阶有f(n)种跳法。在所有跳法中，青蛙的最后一步只有两种情况： 跳上1级或2级台阶。
    1. 当为1级台阶： 剩n−1个台阶，此情况共有f(n−1)种跳法;
    2. 当为2级台阶： 剩n−2个台阶，此情况共有f(n−2)种跳法;
    3. 即 f(n) = f(n-1) + f(n-2)
复杂度
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int numWays(int n) {
        int MOD = 1000000007;
        if (n == 0) return 1;
        if (n < 3) return n;

        int p = 1;
        int q = 1;
        int r = 2;
        for (int i=3; i<=n; i++) {
            p = q;
            q = r;
            r = (p + q) % MOD;
        }
        return r;
    }
}

剑指 Offer 46. 把数字翻译成字符串

动态规划

算法流程
  1. 当前长度n的翻译方法个数f(n)，可以看为最后余一位数字的翻译个数f(n-1) + 最后余两位数字的翻译方法个数f(n-2)
  2. 当最后余一位时，肯定可以有一种翻译方式
  3. 当最后余两位x时，这个两位数可能大于25或小于10，就会不成立
  4. 所以最后动态规划转移方程为：f(n) = f(n-1) + f[n-2](10<= x <= 25)
复杂度
  • 时间复杂度：O(n)。
  • 空间复杂度：O(logn)。将数字变成了一个字符串，复杂度为logn
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int translateNum(int num) {
        String src = String.valueOf(num);
        int p = 0, q = 0, r = 1;
        for (int i = 0; i < src.length(); ++i) {
            p = q; 
            q = r; 
            // r = q;
            if (i == 0) {
                continue;
            }
            String pre = src.substring(i - 1, i + 1);
            if (pre.compareTo("25") <= 0 && pre.compareTo("10") >= 0) {
                r += p;
            }
        }
        return r;
    }
}

剑指 Offer 48. 最长不含重复字符的子字符串

剑指 Offer 63. 股票的最大利润

动态规划

算法流程
  1. 初始化：最低价格minprice，最高利润maxprofit
  2. 对价格表遍历：
    1. 当 price[i]<minprice 时，minprice=price[i]
    2. 当卖出价格减最低买入价格大于最大利润时，即price[i] - minprice > maxprofit， maxprofit = price[i - minprice]
  3. return maxprofit。
复杂度
  • 时间复杂度：O(n)。对整个数组遍历一遍
  • 空间复杂度：O(1)。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int maxProfit(int[] prices) {
        int minprice = Integer.MAX_VALUE;
        int maxprofit = 0;
        for (int i=0; i<prices.length; i++) {
            if (prices[i] < minprice) {
                minprice = prices[i];
            } else if (prices[i] - minprice > maxprofit) {
                maxprofit = prices[i] - minprice; 
            }
        }
        return maxprofit;
    }
}

双指针

剑指 Offer 21. 调整数组顺序使奇数位于偶数前面

双指针(自己)

算法流程
  1. 初始化：new一个与nums同样大小的数组res[]
  2. 设置两个指针，一个指向res开头，一个指向结尾
  3. 遍历整个数组nums，判断每一个数字
    1. 若为奇数，放在res[i]，i++；
    2. 若为偶数，放在res[j]，j–；
  4. return res;
复杂度
  • 时间复杂度：O(n)。需遍历整个数组
  • 空间复杂度：O(n)。需要额外的一个数组长度的空间
代码
1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public int[] exchange(int[] nums) {
        int i = 0, j = nums.length - 1;
        int[] res = new int[j+1];
        for (int num : nums) {
            if (num % 2 == 1) res[i++] = num;
            else res[j--] = num;
        }
        return res;
    }
}

双指针

算法流程
  1. 初始化：两个指针i和j，一个指向数组开头，一个指向数组结尾
  2. 当i<j:
    1. 从前到后，知道碰到偶数
    2. 从后往前，直到碰到奇数
    3. 互换两者位置
  3. return nums;
复杂度
  • 时间复杂度：O(n)。相当于遍历了整个数组
  • 空间复杂度：o(1)。使用了原数组的空间
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int[] exchange(int[] nums) {
        int i = 0, j = nums.length-1, temp;
        while (i < j) {
            while (i < j && nums[i]%2 == 1) i++;
            while (j > i && nums[j]%2 == 0) j--;
            temp = nums[i];
            nums[i] = nums[j];
            nums[j] = temp;
        }
        return nums;
    }
}

剑指 Offer 52. 两个链表的第一个公共节点

双指针

算法流程
  1. 若两个表相交，链表headA和headB的长度分别为m和n。假设相交部分长度为c，headA不相交部分为a，headB不相交部分为b，有a+c=m,b+c=n;
    1. 若a=b，则headA和headB会同时到达相交点；
    2. 若a!=b，headA遍历完整个A链表，在遍历B链表的不相交部分，即遍历a+c+b；headB遍历完整个B链表，然后遍历A的不相交部分，即遍历b+c+a；接下来的一个节点即相交点；
  2. 若两个表不相交
    1. 若a=b，则同时遍历完headA和headB后，同时变为null，此时返回null；
    2. 若a!=b，则遍历完headA+headB后，同时变为null，此时返回null；
复杂度
  • 时间复杂度：O(n)。最短需遍历链表的一部分，最长需要遍历链表A+链表B
  • 空间复杂度：O(1)。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        if (headA==null || headB==null) return null;

        ListNode pA = headA;
        ListNode pB = headB;
        while (pA != pB) {
            pA = pA==null ? headB : pA.next;
            pB = pB==null ? headA : pB.next;
        }
        return pA;
    }
}

剑指 Offer 57. 和为s的两个数字

暴力

算法流程
  1. 两层循环，超出时间限制
代码
1
2
3
4
5
6
7
8
9
10
class Solution {
    public int[] twoSum(int[] nums, int target) {
        for (int i=0; i<nums.length; i++) {
            for (int j=0; j<nums.length; j++) {
                if (nums[i] + nums[j] == target) return new int[] {nums[i], nums[j]};
            }
        }
        return new int[0];
    }
}

双指针

算法流程
  1. 初始化：设置两个指针，一个指向开头，一个指向结尾
  2. 当i < j：
    1. 若 nums[i]+nums[j] < target: i++;
    2. 若 nums[i]+nums[j] > target: j–;
    3. 若 nums[i]+nums[j] = target: 返回这两个值
  3. 没有符合的就返回null
复杂度
  • 时间复杂度：O(n)。需要遍历整个数组
  • 空间复杂度：O(1)。
代码
1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public int[] twoSum(int[] nums, int target) {
        int i = 0, j = nums.length-1;
        while (i < j) {
            if (nums[i] + nums[j] > target) j--;
            else if (nums[i] + nums[j] < target) i++;
            else return new int[] {nums[i], nums[j]};
        }
        return new int[0];
    }
}

剑指 Offer 58 - I. 翻转单词顺序

双指针

算法流程
  1. 初始化：设置两个指针，均指向s的结尾，new一个StringBuilder；
  2. 当 i>=0 时：
    1. j指向字符串当前单词的结尾，i不为 ‘ ‘ 空格时，i–，直到到达当前单词的开头，截取此单词append到StringBuilder中；
    2. 将j指向前一个单词的结尾
  3. return StringBuilder.tostring().trim(); trim是去掉多余空格
复杂度
  • 时间复杂度：O(n)。需遍历整个数组
  • 空间复杂度：O(n)。需额外StringBuilder大小的空间
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public String reverseWords(String s) {
        s = s.trim();
        StringBuilder res = new StringBuilder();
        int i = s.length() - 1, j = i;
        while (i >= 0) {
            while (i>=0 && s.charAt(i) != ' ') i--;
            res.append(s.substring(i+1, j+1) + " ");
            while (i>=0 && s.charAt(i) == ' ') i--;
            j = i;
        }
        return res.toString().trim();
    }
}

搜索和回溯算法

12. 矩阵中的路径

回溯

算法流程

exist函数

  1. 两层for循环遍历整个矩阵：
    1. 使用dfs函数判断是否存在路径，若存在直接返回true
    2. 否则最后返回false

dfs函数

  1. 传入参数，当前元素在矩阵border的行列索引i和j，当前目标字符在words中的索引
  2. 终止条件：
    1. 返回false，1.行或列索引越界 2.当前元素与目标字符不同
    2. 返回true，k = words.length-1，即字符串word已经全部匹配
  3. 递推：
    1. 标记当前元素：将border[i][j]修改为 ‘\0’，代表当前元素已访问过
    2. 搜索下一单元格：朝当前元素的 下 右 上 左 四个方向进行递归，使用 || 连接，表示只要找到一条可行路径就直接返回，不再继续后续的dfs，并记录结果至res
    3. 还原当前矩阵元素：border[i][j] = works[k]
复杂度
  • 时间复杂度：O(3^n)。两层for循环复杂度为O(n^2)，递归需要朝着三个方向(上个字符的方向被丢弃)，即O(3^n)
  • 空间复杂度：O(K)。搜索过程中的递归深度不超过 K ，因此系统因函数调用累计使用的栈空间占用 O(K) （因为函数返回后，系统调用的栈空间会释放）。最坏情况下 K = MN ，递归深度为 MN，此时系统栈使用 O(MN) 的额外空间。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public boolean exist(char[][] board, String word) {
        char[] words = word.toCharArray();
        for (int i=0; i<board.length; i++) {
            for (int j=0; j<board[0].length; j++) {
                if (dfs(board, words, i, j, 0)) return true;
            }
        }
        return false;
    }

    public boolean dfs(char[][] board, char[] words, int i, int j, int k) {
        // 判断第一位相不相同
        if (i>=board.length || i<0 || j>=board[0].length || j<0 || board[i][j]!=words[k]) return false;
        // 遍历完整个words后
        if (k == words.length-1) return true;

        board[i][j] = '\0';
        // 下 右 上 左
        boolean res = dfs(board, words, i+1, j, k+1) || dfs(board, words, i, j+1, k+1) || dfs(board, words, i-1, j, k+1) || dfs(board, words, i, j-1, k+1);
        board[i][j] = words[k];
        return res;
    }
}

13. 机器人的运动范围

回溯 + DFS

算法流程
  1. 递归参数： 当前元素在矩阵中的行列索引 i 和 j ，两者的数位和 di, dj 。
  2. 终止条件： 当 行列索引越界 或 数位和超出目标值 k 或 当前元素已访问过 时，返回 0 ，代表不计入可达解。
  3. 递推工作：
    1. 标记当前单元格 ：将索引 (i, j) 存入 Set visited 中，代表此单元格已被访问过。
    2. 搜索下一单元格： 计算当前元素的 下、右 两个方向元素的数位和，并开启下层递归 。
  4. 回溯返回值： 返回 1 + 右方搜索的可达解总数 + 下方搜索的可达解总数，代表从本单元格递归搜索的可达解总数。
复杂度

设矩阵行列数分别为 M, N 。

  • 时间复杂度：O(MN)。最差情况，机器人遍历矩阵所以单元格
  • 空间复杂度:O(MN)。使用额外M*N大小的visited的空间
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    int m, n, k;
    boolean[][] visited;
    public int movingCount(int m, int n, int k) {
        this.m = m; this.n = n; this.k = k;
        this.visited = new boolean[m][n];
        return dfs(0, 0, 0, 0);
    }

    public int dfs(int i, int j, int di, int dj) {
        if (i>=m || j>=n || di+dj>k || visited[i][j]) return 0;
        visited[i][j] = true;
        return 1 + dfs(i+1, j, (i+1)%10==0? di-8:di+1, dj) + dfs(i, j+1, di, (j+1)%10==0? dj-8:dj+1);
    }
}

BFS

算法流程
  1. 初始化：将机器人的初始点(0,0)加入队列 queue;res统计可达解的数量
  2. 迭代终止条件：queue为空时，代表遍历完所有可达解;
  3. 进行迭代：
    1. 单元格出队：将队首元素的 索引、数位和 弹出，作为当前搜索的单元格
    2. 判断是否跳过：若 行列索引越界 或 数位和超出目标值k 或当前元素已访问过，执行continue
    3. 标记当前单元格：visited[i][j]标记为true，res+1
    4. 单元格入队：当前元素的下方、右方单元格的索引和数位和加入queue
  4. return res;
复杂度
  • 时间复杂度：O(MN)。
  • 空间复杂度：O(MN)。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int movingCount(int m, int n, int k) {
        boolean[][] visited = new boolean[m][n];
        int res = 0;
        Queue<int[]> queue = new LinkedList<>();
        queue.add(new int[] {0, 0, 0, 0});
        while (queue.size() > 0) {
            int[] x = queue.poll();
            int i = x[0], j = x[1], di = x[2], dj = x[3];
            if (i>=m || j>=n || di+dj>k || visited[i][j]) continue;
            visited[i][j] = true;
            res++;
            queue.add(new int[] {i+1, j, (i+1)%10==0?di-8:di+1, dj});
            queue.add(new int[] {i, j+1, di, (j+1)%10==0?dj-8:dj+1});
        }
        return res;
    }
}

34. 二叉树中和为某一值的路径

DFS

算法流程
  1. 初始化：一个返回值res，存储路径上的值，一个path
  2. 递推参数：根节点root和tar
  3. 递推工作：
    1. 路径更新： 将当前节点值 root.val 加入路径 path ；
    2. 目标值更新： tar = tar - root.val（即目标值 tar 从 sum 减至 0 ）；
    3. 路径记录： 当 root 为叶节点 且 路径和等于目标值 ，则将此路径 path 加入 res 。
    4. 先序遍历： 递归左 / 右子节点。
    5. 路径恢复： 向上回溯前，需要将当前节点从路径 path 中删除，即执行 path.pop() 。
复杂度
  • 时间复杂度：O(n)。
  • 空间复杂度：O(n)。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    List<List<Integer>> res = new LinkedList<>();
    Deque<Integer> path = new LinkedList<>();
    public List<List<Integer>> pathSum(TreeNode root, int target) {
        dfs(root, target);
        return res;
    }

    public void dfs(TreeNode root, int target) {
        if (root == null) return;
        path.offerLast(root.val);
        target -= root.val;
        if (root.left == null && root.right == null && target == 0) {
            res.add(new LinkedList<Integer>(path));
        }
        dfs(root.left, target);
        dfs(root.right, target);
        path.pollLast();
    }
}

BFS

排序

40. 最小的k个数

Arrays的函数

算法流程
  1. 排序sort
  2. 取前k个数
复杂度
  • 时间复杂度：O(nlogn)。复杂度就是sort排序的复杂度
  • 空间复杂度：O(k)=O(1)。
代码
1
2
3
4
5
6
class Solution {
    public int[] getLeastNumbers(int[] arr, int k) {
        Arrays.sort(arr);
        return Arrays.copyOfRange(arr, 0, k);
    }
}

快排

占位

61. 扑克牌中的顺子

集合Set + 遍历

算法流程
  1. 初始化：new一个hashset，存储数值，max和min存储nums的最大值和最小值（除0外）
  2. 进行遍历：
    1. 当num为0时，直接跳过
    2. 如果存在重复的元素，return false
    3. 获得最大值和最小值
    4. 将num加入repeat
  3. 返回 max-min<5 的结果
复杂度
  • 时间复杂度：O(1)。题目中的nums只会出现5个数字，遍历只需要O(N)=O(5)=O(1);
  • 空间复杂度：O(1)。只有最多额外存储nums长度的set
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public boolean isStraight(int[] nums) {
        Set<Integer> repeat = new HashSet<>();
        int max = 0, min = 14;
        for (int num : nums) {
            if (num == 0) continue;
            max = Math.max(max, num);
            min = Math.min(min, num);
            if (repeat.contains(num)) return false;
            repeat.add(num);
        }
        return max - min < 5;
    }
}

排序 + 遍历

算法流程
  1. 对数组进行排序
  2. 遍历数组：
    1. 当有重复时，return false
    2. 获得joker的数量
  3. 所以，nums[4]为最大值，nums[joker]为除joker外最小的值
  4. return nums[4]-nums[joker] < 5
复杂度
  • 时间复杂度：O(1)。sort的复杂度为O(nlogn)，但是n为5，所以复杂度为O(1)
  • 空间复杂度：O(1)。并不需要额外的空间
代码
1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public boolean isStraight(int[] nums) {
        int joker = 0;
        Arrays.sort(nums);
        for (int i=0; i<4; i++) {
            if (nums[i] == 0) joker++;
            else if (nums[i] == nums[i+1]) return false;
        }
        return nums[4]-nums[joker] < 5;
    }
}

位运算

15. 二进制中1的个数

循环遍历二进制位

算法流程
  1. 初始化：res记录 1 的位数
  2. 遍历二进制位的每一位
    1. 当与 1 相交不为 0 时，说明该位为 1，res++；
  3. return res
复杂度
  • 时间复杂度：O(k)=O(1)。一共只需检查32位
  • 空间复杂度：O(1)。
代码
1
2
3
4
5
6
7
8
9
10
public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        int res = 0;
        for (int i=0; i<32; i++) {
            if ((n & (1 << i)) != 0) res++;
        }
        return res;
    }
}
优化后
1
2
3
4
5
6
7
8
9
10
11
public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        int res = 0;
        while (n != 0) {
            n &= n-1;
            res++;
        }
        return res;
    }
}
  • 时间复杂度：O(logn)。循环次数等于 n 的二进制位中 1 的个数，最坏情况下 n 的二进制位全部为 1。我们需要循环 logn 次。

56 - I. 数组中数字出现的次数

位运算

算法流程
  1. 不想写流程了
复杂度
  • 时间复杂度：O(n)。
  • 空间复杂度：O(1)。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int[] singleNumbers(int[] nums) {
        int temp = 0;
        for (int num : nums) {
            temp ^= num;
        }
        int m = 1;
        while ((temp & m) == 0) {
            m <<= 1; // 区分两个单次出现的数字，关键
        }

        int x = 0, y = 0;
        for (int num : nums) {
            if ((m & num) == 0) x ^= num;
            else y ^= num;
        }
        return new int[] {x, y};
    }
}

56 - II. 数组中数字出现的次数 II

哈希表

算法流程
  1. 初始化：建立一个哈希表，存放数字和出现的次数
  2. 遍历数组nums，将出现的数字的次数放入哈希表中
  3. 返回出现次数为1的值
复杂度
  • 时间复杂度：O(n)。遍历真个数组
  • 空间复杂度：O(n)。会额外占用 (n-1)/3 + 1 的额外空间
代码
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int singleNumber(int[] nums) {
        Map<Integer, Integer> count = new HashMap<>();
        for (int num : nums) {
            count.put(num, count.getOrDefault(num, 0) + 1);
        }
        for (int num : nums) {
            if (count.get(num) == 1) return num;
        }
        return 0;
    }
}

65. 不用加减乘除做加法

位运算

算法流程
  1. 用异或 ^ 表示和，用与 & 表示进位
复杂度
  • 时间复杂度：O(1)。最差情况下（例如 a = 0x7fffffff , b = 1 时），需进位31次，即循环 32 次，使用 O(1) 时间；每轮中的常数次位操作使用 O(1) 时间。
  • 空间复杂度：O(1)。
代码
1
2
3
4
5
6
7
8
9
10
class Solution {
    public int add(int a, int b) {
        while (b != 0) {
            int c = (a & b) << 1;
            a ^= b;
            b = c;
        }
        return a;
    }
}

数学

剑指 Offer 4- I. 剪绳子

数学

代码
1
2
3
4
5
6
7
8
9
class Solution {
    public int cuttingRope(int n) {
        if(n <= 3) return n - 1;
        int a = n / 3, b = n % 3;
        if(b == 0) return (int)Math.pow(3, a);
        if(b == 1) return (int)Math.pow(3, a - 1) * 4;
        return (int)Math.pow(3, a) * 2;
    }
}

剑指 Offer 39. 数组中出现次数超过一半的数字

HashMap

算法流程
  1. 使用hashmap统计每个数字出现的次数
  2. 当存在一个数字出现次数大于数组长度的一半时，return num；
复杂度
  • 时间复杂度：O(n)。最差情况遍历整个数组
  • 空间复杂度：O(n)。最差使用额外n/2大小的空间
代码
1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public int majorityElement(int[] nums) {
        Map<Integer, Integer> map = new HashMap<>();
        int half = nums.length / 2;
        for (int num : nums) {
            map.put(num, map.getOrDefault(num, 0) + 1);
            if (map.get(num) > half) return num;
        }
        return 0;
    }
}

剑指 Offer 57 - II. 和为s的连续正数序列

双指针

算法流程
  1. 初始化：一个存放返回的链表，两个指针l和r
  2. 当左指针 < 右指针时：
    1. 计算左指针到右指针区间的值的sum
    2. 若sum==target，将l一直到r的数字的放入一个临时数组加到链表中，并且l++
    3. 若sum < target，r++
    4. 若sum > target，l++
  3. 将链表转为数组，并返回
复杂度
  • 时间复杂度：O(n)。
  • 空间复杂度：O(1)。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int[][] findContinuousSequence(int target) {
        List<int[]> res = new LinkedList<>();
        for (int l=1, r=2; l<r;) {
            int sum = (l + r) * (r - l + 1) / 2;
            if (sum == target) {
                int[] temp = new int[r-l+1];
                for (int i=0; i<r-l+1; i++) {
                    temp[i] = l + i;
                }
                res.add(temp);
                l++;
            } else if (sum < target) {
                r++;
            } else {
                l++;
            }
        }
        return res.toArray(new int[res.size()][]);
    }
}

剑指 Offer 66. 构建乘积数组

暴力法

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int[] constructArr(int[] a) {
        int[] arr = new int[a.length];
        for (int i=0; i<a.length; i++) {
            int temp = 1;
            for (int j=0; j<a.length; j++) {
                if (i != j) temp *= a[j]; 
            }
            arr[i] = temp;
        }
        return arr;
    }
}

数字

算法流程
  1. 分为上三角和下三角
  2. 先计算下三角，然后用一个临时数再乘进去
复杂度
  • 时间复杂度：O(n)。只需遍历数组两遍
  • 空间复杂度：O(n)。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int[] constructArr(int[] a) {
        int len = a.length;
        if (len == 0) return new int[0];
        int[] arr = new int[len];
        int temp = a[len-1];
        arr[0] = 1;
        for (int i=1; i<len; i++) {
            arr[i] = arr[i-1] * a[i-1];
        }
        for (int i=len-1-1; i>=0; i--) {
            arr[i] *= temp;
            temp *= a[i]; 
        }
        return arr;
    }
}
  • 本文标题：剑指Offer
  • 本文作者：Kang
  • 创建时间：2021-04-14 19:55:54
  • 本文链接：ykhou.github.io2021/04/14/剑指Offer/
  • 版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！